Let's say there are two code snippets code 1 and code 2, both of which take x and y seconds to get completed.
Given the statement, one can say that if x<y, then code 1 performs faster than code 2 and if y<x code 2 performs faster than code 1. But the twist here is these statements are valid only if they are run on the same system, if they are performed on different systems with different computation speeds we can't judge which one is faster by simply measuring the time they require to get run(x,y).
So, the time complexity is no of operations that it takes to complete something.
So when u deal with time complexity, they are associated with three Greek letters, Omega(Ω), Theta(Θ), and Omicron(Ο).
Ω -> best case
Θ -> average case
Ο -> worst case
let's understand using the Time module in Python
import time
n=10000
t1=time.time()
for i in range(n):
pass
t2=time.time()
print(t2-t1)
output for the above program in python compiler -> 0.00154 seconds
if we increase n 10 times (i.e n=20000), output for the above program in python compiler -> 0.00314 seconds
as the no of operations(n) increased the time taken also increased.
so we can infer this as O(n) as in the worst case it will compile all the operations and the no of operations are n simply, so O(n).
Let's talk about O(log n)
let's say we have a list of over a million items, let's say 1132096 elements are there in the list, and we need to find the element in the list, for a worst case we need to perform over a million operations if we search the element iteratively but we know that,
if we go for another approach like binary search then we split the list into halves and then search in them accordingly, by diving into two halves and so on.
so if we have 8 elements then we can find the desired element in worst case scenario in almost 3 iterations using binary search
As 2^3=8 then log(8) to the base of 2 will be equal to 3
in the above case log(1132096) to the base of 2 will be equal to 20
so instead of using over a million operations to find an element we can use binary search and find that element in at most 20 operations.
since n is the no of operations so O(log n)
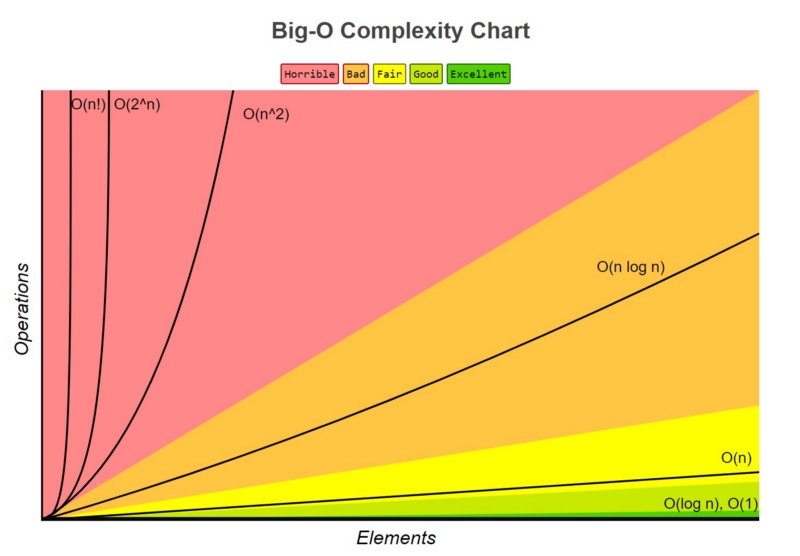
here is a graphical representation of a comparison of various Big O's